Method of complements

In mathematics and computing, the method of complements is a technique used to subtract one number from another using only addition of positive numbers. This method was commonly used in mechanical calculators and is still used in modern computers. To subtract a number y (the subtrahend) from another number x (the minuend), the radix complement of y is added to x and the initial '1' of the result is discarded. Discarding the initial '1' is especially convenient on calculators or computers that use a fixed number of digits: there is nowhere for it to go so it is simply lost during the calculation.

1 Numeric complements
2 Decimal example
3 Binary example
4 Negative number representations
5 Practical uses
6 In elementary education
7 Notes

Numeric complements

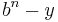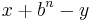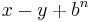The radix complement of an n digit number y in radix b is, by definition, $b^n-y$ . Adding this to x results in the value $x%2Bb^n-y$ or $x-y%2Bb^n$ . Assuming y ≤ x, the result will always be greater or equal to 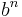$b^n$ and dropping the initial '1' is the same as subtracting 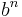$b^n$ , making the result 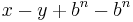$x-y%2Bb^n-b^n$ or just 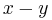$x-y$ , the desired result.

The radix complement is most easily obtained by adding 1 to the diminished radix complement, which is 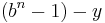$(b^n-1)-y$ . Since 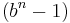$(b^n-1)$ is the digit 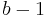$b-1$ repeated n times (because 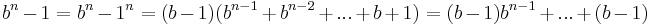$b^n-1 = b^n-1^n = (b-1)(b^{n-1}%2Bb^{n-2}%2B...%2Bb%2B1)=(b-1)b^{n-1}%2B...%2B(b-1)$ , see also binomial numbers), the diminished radix complement of a number is found by complementing each digit with respect to 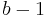$b-1$ (that is, subtracting each digit in y from 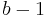$b-1$ ). Adding 1 to obtain the radix complement can be done separately, but is most often combined with the addition of x and the complement of y.

In the decimal numbering system, the radix complement is called the ten's complement and the diminished radix complement the nines' complement. In binary, the radix complement is called the two's complement and the diminished radix complement the ones' complement. The naming of complements in other bases is similar. Some people, notably Donald Knuth, recommend using the placement of the apostrophe to distinguish between the radix complement and the diminished radix complement. In this usage, the four's complement refers to the radix complement of a number in base four while fours' complement is the diminished radix complement of a number in base 5. However, the distinction is not important when the radix is apparent (nearly always), and the subtle difference in apostrophe placement is not common practice. Most writers use one's and nine's complement, and many style manuals leave out the apostrophe, recommending ones and nines complement.

Decimal example

To subtract a decimal number y from another number x using the method of complements, the ten's complement of y (nines' complement plus 1) is added to x. Typically, the nines' complement of y is first obtained by determining the complement of each digit. The complement of a decimal digit in the nines' complement system is the number that must be added to it to produce 9. The complement of 3 is 6, the complement of 7 is 2, and so on. Given a subtraction problem:

  873  (x, the minuend)
- 218  (y, the subtrahend)

The nines' complement of y (218) is 781. In this case, because y is three digits long, this is the same as subtracting y from 999.

Next, the sum of x, the nines' complement of y, and 1 is taken:

  873  (x)
+ 781  (nines' complement of y)
=====
 1654
-1000  (y + nines' complement of y) + 1 or (y + tens' complement of y)
=====
  654

The first "1" digit is then dropped, in an effort to keep the same digits as the original, giving 654. This is not yet correct. We have essentially added 999 to the equation in the first step. Then we remove 1000 when we drop the first 1 in the answer (above) this will make the answer we get one less than the correct answer. To fix this, we must add 1 to the answer.

 654
  +1
====
 655

Adding a 1 gives 655, the correct answer.

If the subtrahend has fewer digits than the minuend, leading zeros must be added which will become leading nines when the complement is taken. For example:

  48032  (x)
-   391  (y)

becomes the sum:

  48032  (x)
+ 99608  (nines' complement of y)
=======
 147640

Dropping the "1" yields 47640, and adding the dropped "1" to 47640 gives the answer: 47641.

Binary example

The method of complements is especially useful in binary (radix 2) since the ones' complement is very easily obtained by inverting each bit (changing '0' to '1' and vice versa). And adding 1 to get the two's complement can be done by simulating a carry into the least significant bit. For example:

  01100100  (x, equals decimal 100)
- 00010110  (y, equals decimal 22)

becomes the sum:

  01100100  (x)
+ 11101001  (ones' complement of y)
+        1  (to get the two's complement)
==========
 101001110

Dropping the initial "1" gives the answer: 01001110 (equals decimal 78)

Negative number representations

Main article: Signed number representations

The method of complements normally assumes that the operands are positive and that y ≤ x, logical constraints given that adding and subtracting arbitrary integers is normally done by comparing signs, adding the two or subtracting the smaller from the larger, and giving the result the correct sign.

Let's see what happens if x < y. In that case, there will not be a "1" digit to cross out after the addition since 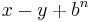$x-y%2Bb^n$ will be less than 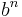$b^n$ . For example (in decimal):

  185  (x)
- 329  (y)

Complementing y and adding gives:

  185  (x)
+ 670  (nines' complement of y)
+   1
=====
  856

This is obviously the wrong answer; the expected answer is -144. But it isn't as far off as it seems; 856 happens to be the ten's complement of 144. This issue can be addressed in three ways:

Ignore the issue. This is reasonable if a person is operating a calculating device that doesn't support negative numbers since comparing the two operands before the calculation so they can be entered in the proper order, and verifying that the result is reasonable, is easy for humans to do.
Represent negative numbers as radix complements of their positive counterparts. Numbers less than 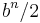$b^n/2$ are considered positive; the rest are considered negative (and their magnitude can be obtained by taking the radix complement). This works best for even radices since the sign can be determined by looking at the first digit. For example, numbers in ten's complement notation are positive if the first digit is 0, 1, 2, 3, or 4, and negative if 5, 6, 7, 8, or 9. And it works very well in binary since the first bit can be considered a sign bit: the number is positive if the sign bit is 0 and negative if it is 1. Indeed, two's complement is used in most modern computers to represent signed numbers.
Complement the result if there is no carry out of the most significant digit (an indication that x was less than y). This is easier to implement with digital circuits than comparing and swapping the operands. But since taking the radix complement requires adding 1, it is difficult to do directly. Fortunately, a trick can be used to get around this addition: Instead of always setting a carry into the least significant digit when subtracting, the carry out of the most significant digit is used as the carry input into the least significant digit (an operation called an end-around carry). So if y ≤ x, the carry from the most significant digit that would normally be ignored is added, producing the correct result. And if not, the 1 is not added and the result is one less than the radix complement of the answer, or the diminished radix complement, which does not require an addition to obtain. This method is used by computers that use sign-and-magnitude to represent signed numbers.

Practical uses

The method of complements was used in many mechanical calculators as an alternative to running the gears backwards. For example:

Pascal's calculator had two sets of results digits, a black set displaying the normal result and a red set displaying the nines' complement of this. A horizontal slat was used to cover up one of these sets, exposing the other. To subtract, the red digits were exposed and set to 0. Then the subtrahend (the number being subtracted) was dialed in. The slat was then moved to expose the black digits (which now displayed the nines' complement of the subtrahend) and the minuend was added by dialing it in. Finally, the operator had to mentally add 1 and ignore the leftmost 1 to obtain the correct answer.

The Comptometer had nines' complement digits printed in smaller type along with the normal digits on each key. To subtract, the operator was expected to mentally subtract 1 from the subtrahend and enter the result using the smaller digits. Since subtracting 1 before complementing is equivalent to adding 1 afterwards, the operator would thus effectively add the ten's complement of the subtrahend. The operator also needed to hold down the "subtraction cutoff tab" corresponding to the leftmost digit of the answer. This tab prevented the carry from being propagated past it, the Comptometer's method of dropping the initial 1 from the result.

The Curta calculator used the method of complements for subtraction, and managed to hide this from the user. Numbers were entered using digit input slides along the side of the device. The number on each slide was added to a result counter by a gearing mechanism which engaged cams on a rotating "echelon drum" (a.k.a. "step drum"). The drum was turned by use of a crank on the top of the instrument. The number of cams encountered by each digit as the crank turned was determined by the value of that digit. For example, if a slide is set to its "6" position, a row of 6 cams would be encountered around the drum corresponding to that position. For subtraction, the drum was shifted slightly before it was turned, which moved a different row of cams into position. This alternate row contained the nines' complement of the digits. Thus, the row of 6 cams that had be in position for addition now had a row with 3 cams. The shifted drum also engaged one extra cam which added 1 to the result (as required for the method of complements). The always present tens' complement "overflow 1" which carried out beyond the most significant digit of the results register was, in effect, discarded.

Use of the method of complements is ubiquitous in digital computers, regardless of the representation used for signed numbers. However, the circuitry required depends on the representation:

If two's complement representation is used, subtraction requires only inverting the bits of the subtrahend and setting a carry into the rightmost bit.

Using ones' complement representation requires inverting the bits of the subtrahend and connecting the carry out of the most significant bit to the carry in of the least significant bit (end-around carry).

Using sign-magnitude representation requires only complementing the sign bit of the subtrahend and adding, but the addition/subtraction logic needs to compare the sign bits, complement one of the inputs if they are different, implement an end-around carry, and complement the result if there was no carry from the most significant bit.

The method of complements was used to correct errors when accounting books were written by hand. To remove an entry from a column of numbers, the accountant could add a new entry with the ten's complement of the number to subtract. A bar was added over the digits of this entry to denote its special status. It was then possible to add the whole column of figures.

Complementing the sum is handy for cashiers making change for a purchase from currency in a single denomination of 1 raised to an integer power of the currency's base. For decimal currencies that would be 10, 100, 1,000, etc., e.g. a $10.00 bill.

In elementary education

In grade schools, students are sometimes taught the method of complements as a shortcut useful in mental arithmetic.^[1] Subtraction is done by adding the ten's complement of the subtrahend, which is the nines' complement plus 1. The method is generally only applied when it is clear that the difference will be positive. The same technique works for subtracting on an adding machine.

Notes

^ Carl Barnett Allendoerfer (1971). Principles of Arithmetic and Geometry for Elementary School Teachers. Macmillan.